A Developer's Notebook

In our last installment on trees, we studied and implemented the AVL tree. The AVL tree is one of many self-balancing binary search trees, a special kind of BST that enforces sub-linear operation costs by maintaining tree height close to the theoretical minimum of $latex log_{2}(n)$. This is usually done by what is called tree rotation, which is basically moving around tree nodes (and updating some special node properties).

As you can see in the Wikipedia page¹, AVL trees guarantee that the tree height is strictly less than $latex \approx 1.44~log_{2}(n)$, while Red-black trees have a slightly worse threshold of $latex \approx 2~log_{2}(n)$; thus, AVL trees will provide significantly better search times than Red-black trees. However, while AVL trees may need to do $latex O(log(n))$ rotations after each insertion, Red-black trees must do at most 2 rotations per insertion. So either one may be your tree of choice depending on the application: if search time is critical but data doesn’t get updated too often, an AVL tree will perform better; whereas a Red-black tree will perform better in scenarios where data is constantly being changed.

Self-balancing BSTs add some kind of property to tree nodes that make way for tree balancing: with AVL trees, it was the “balance factor”. With Red-black trees, a “color” property is added to each node. This leads us to the Red-black tree properties:

Every node is either red or black
Every leaf is black
If a node is red, then both its children are black
Every path from a node to any of its descendant leafs contains the same number of black nodes

These four properties are sufficient to enforce that tree height is always less than $latex \approx 2~log_{2}(n)$. These properties are maintained by applying tree rotations (which are very similar to the ones performed in AVL trees) and by swapping node colors. The concept of Red-black trees is deceivingly simple, whilst implementation can become complicated, even more so in C, our language of choice for this kind of stuff.

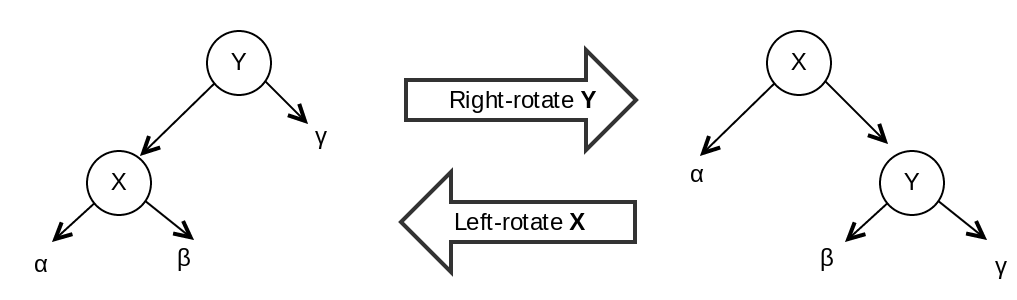
Unlike AVL trees, Red-black trees have only two of rotations, left and right, depicted in the figure below:

red_black_tree_rotatio

As you may have figured, these rotations can potentially violate rules 3 and 4, so after each rotation we’ll have to check the resulting subtree nodes’ colors for violations. Let’s see some examples before going through the code:

red_black_right_rotat

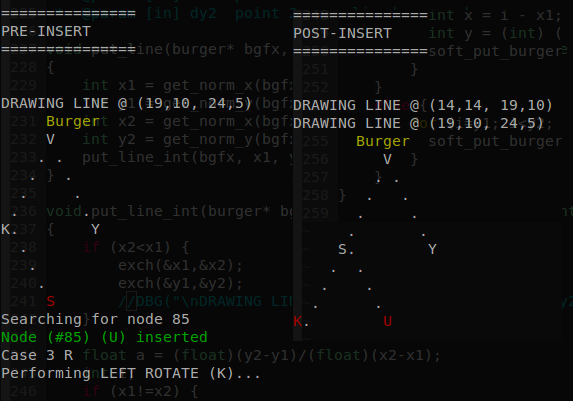
Here we have a Red-black tree rooted on node W (which is black). We then add M to the tree. Since M < P < W, it is added as a left child of P. All new nodes are red², so rule 3 is violated (P is red and has a red child, M); thus, a right-rotate is performed on W (on our diagram, Y = W, X = P, alpha = M and the rest are null pointers). For convenience, the tree root is always painted black after each insertion (to avoid violation of rule 3). Let’s see another example, now with left rotation:

red_black_left_rotat

Node U is inserted as a right child of S, violating rule 3 again, and the subtree K < S < U is left-rotated. However, even after rotation rule 3 is still violated, since S and U are both red. Rule 4 is violated as well: since K is black and U is red, S has paths with different amounts of black nodes (2 on the left and 1 on the right - remember than null leafs count as black nodes). This is fixed by swapping K and S’s colors (‘Case 3 R’ as seen in the terminal).

When inserting a new node in a Red-black tree, there are in total 6 situations where rotations and color changes are needed, but half are symmetric. Here is the insertion pseudocode identifying the 3 cases:

def red_black_insert(value, tree)
  node n = tree.bst_insert(value)
  n.set_red
  while ((tree.root != n) && parent(n).is_red)
    if grandfather(n).left == parent(n)
      if grandfather(n).right.is_red     # Case 1
        parent(n).set_black
        grandfather(n).right.set_black
        grandfather(n).set_red
        n = grandfather(n)
      else
        if n == parent(n).right          # Case 2
          n = parent(n)
          left_rotate(n)
        parent(n).set_black              # Case 3
        grandfather(n).set_red
        right_rotate(n)
    elif grandfather(n).right == parent(n)
      // Symmetric cases
  tree.root.set_black

As usual, source code in C can be found in our Github repo. Simple testing is provided here (renders the tree in colored ASCII as seen in this post). Only insertion is implemented for now (as is the case with AVL); hopefully I’ll implement deletion in the future.

Notes

1 https://en.wikipedia.org/wiki/AVL_tree#Comparison_to_other_structures

2 This choice may seem arbitrary, but definitively helps us to not violate rule 4, which is potentially more complicated to enforce than rule 3.

Trees, part III - Red-black tree

Notes