render(‘/image.*’, caption: ‘Bright green tree - Waikat’, src: ‘//upload.wikimedia.org/wikipedia/commons/thumb/f/f6/Bright_green_tree_-Waikato.jpg/512px-Bright_green_tree-Waikato.jpg)](http://commons.wikimedia.org/wiki/File%3ABright_green_tree-_Waikato.jpg)
We used trees to build the heap data structure before, but we didn’t bother with the theory behind trees, which are abstract and concrete data structures themselves. There’s a huge range of material to cover so I’ll split this in several posts.
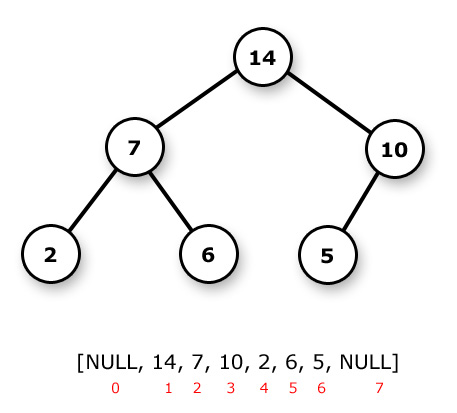
In this first post we’ll cover the basic theory and implement a binary search tree (BST), which provides O(h) time search, insert and delete operations (h is the tree height). First, the basics:
Trees are graphs with a few extra properties and interpretations/conventions. * Trees have height (longest branch length) and depth (distance to root). * The uppermost level consists of at most one node (the tree root). * All nodes may have children. * There are no edges other than parent-child edges.
Trees are classified according to some of those properties above and some others we’ll mention later. Most commonly, there is a constraint to the maximum number of children per node -e.g. the binary tree limits children to 2 per node.